Solver4J – SOCP - second order cone programming

A minimization problem in the form of:

  minimize_x f^Tx  s.t.
    ||A_ix+b_i||₂ ≤ c_i^Tx+d_i,  i=1,...,m
    Fx = g,

where x ∈ Rⁿ, f ∈ Rⁿ, A_i ∈ R^kiXn, b_i ∈ R^ki, c_i ∈ Rⁿ, d_i ∈ R and F ∈ R^pXn

is called a second-order cone program (SOCP). See S.Boyd and L.Vandenberghe, "Convex Optimization", 4.4.2 for more details. The norm appearing in the constraints is the standard Euclidean norm, i.e., ||u||₂ = (u^Tu)^1/2.

We call a constraint of the form

||Ax+b||₂ ≤ c^Tx+d,

where A ∈ R^kXn, a second-order cone constraint of dimension k+1 because it is the same as requiring the affine function x→(Ax+b,c^Tx+d) from Rⁿ to R^k+1 to lie in the second order cone in R^k+1. The second-order cone is also known by several other names: it is called the quadratic cone since it is defined by a quadratic inequality, or it is also called the Lorentz cone or ice-cream cone. The following image shows a second-order cone in R³:

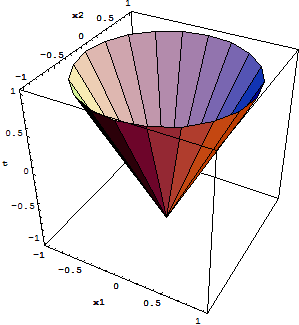
When c_i=0, i=1,...,m, the SOCP is equivalent to a QCQP (which is obtained by squaring each of the constraints). Similarly, if A_i=0, i=1,...,m, then the SOCP reduces to a LP.

You can use the Barrier Method algorithm available with Solver4J for solving this type of problems, passing in the generalized barrier function for the second-order cone in R^k+1 as the barrier function (see S.Boyd and L.Vandenberghe, "Convex Optimization", p. 600):

$Φ (x) = - \sum_{i = 1}^{m} \log ({(c_{i}^{T} x + d_{i})}^{2} - {|| A_{i} x + b_{i} ||}_{2}^{2})$

with

domΦ = {x | {||A_{i} x + b_{i}||}_{2} < c_{i}^{T} x + d_{i}, i = 1,. .., m}

. For strictly feasible x the gradient is equal to

$∇Φ = \sum_{i = 1}^{m} \frac{2}{t_{i}^{2} - u_{i}^{T} u_{i}} J_{i} . [\begin{matrix} u_{i} \\ - t_{i} \end{matrix}]$

and the hessian is

$\nabla^{2} Φ = \sum_{i = 1}^{m} \frac{2}{{(t_{i}^{2} - u_{i}^{T} u_{i})}^{2}} J_{i} . [\begin{matrix} (t_{i}^{2} - u_{i}^{T} u_{i}) I + 2 u_{i} u_{i}^{T} & - 2 t_{i} u_{i} \\ - 2 t_{i} u_{i}^{T} & t_{i}^{2} + u_{i}^{T} u_{i} \end{matrix}] . J_{i}^{T}$

where

$t_{i} = c_{i}^{T} x + d_{i}$ , $u_{i} = A_{i} x + b_{i}$ and $J_{i} = [\begin{matrix} A_{i}^{T} & c_{i} \end{matrix}]$

This function is represented in Solver4J with the class SOCPLogarithmicBarrier.

2D example

Consider the problem graphically represented hereafter: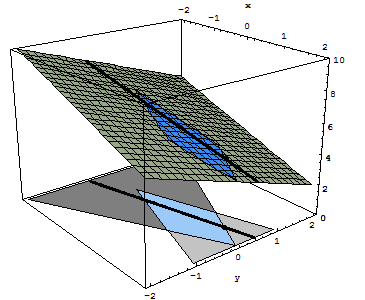

We are now taking n=2, k=1, f={-1,-1}, F={{1./4.,-1.}} and g={0}. There are 2 second-order cone constraints of dimension 2, i.e:

the lightgrey cone, determined by:
- A1 = {{ 0, 1}}
- b1 = { 0 }
- c1 = { 1/3, 0}
- d1 = 1/3
- -x < 1
the darkgrey cone, determined by:
- A2 = {{ 0, 1. }}
- b2 = {0}
- c2 = {-1/2, 0}
- d2 = 1
- x < 2

The intersection region is colored in blue.
It can be solved like this:

		
		// Objective function (plane)
		double[] c = new double[] { -1., -1. };
		LinearMultivariateRealFunction objectiveFunction = new LinearMultivariateRealFunction(c, 6);
		
		//equalities
		double[][] A = new double[][]{{1./4.,-1.}};
		double[] b = new double[]{0};

		List<SOCPConstraintParameters> socpConstraintParametersList = new ArrayList<SOCPLogarithmicBarrier.SOCPConstraintParameters>();
		SOCPLogarithmicBarrier barrierFunction = new SOCPLogarithmicBarrier(socpConstraintParametersList, 2);

//      second order cone constraint in the form ||A1.x+b1||<=c1.x+d1,
		double[][] A1 = new double[][] {{ 0, 1. }};
		double[] b1 = new double[] { 0 };
		double[] c1 = new double[] { 1./3., 0. };
		double d1 = 1./3.;
		SOCPConstraintParameters constraintParams1 = barrierFunction.new SOCPConstraintParameters(A1, b1, c1, d1);
		socpConstraintParametersList.add(socpConstraintParametersList.size(), constraintParams1);
		
//      second order cone constraint in the form ||A2.x+b2||<=c2.x+d2,
		double[][] A2 = new double[][] {{ 0, 1. }};
		double[] b2 = new double[] { 0};
		double[] c2 = new double[] { -1./2., 0};
		double d2 = 1;
		SOCPConstraintParameters constraintParams2 = barrierFunction.new SOCPConstraintParameters(A2, b2, c2, d2);
		socpConstraintParametersList.add(socpConstraintParametersList.size(), constraintParams2);
        
		//optimization problem
		OptimizationRequest or = new OptimizationRequest();
		or.setF0(objectiveFunction);
		or.setInitialPoint(new double[] { 0., 0.});
		or.setA(A);
		or.setB(b);
		or.setCheckProgressConditions(true);
		
		//optimization
		BarrierMethod opt = new BarrierMethod(barrierFunction);
		opt.setOptimizationRequest(or);
		opt.optimize();

This will give the solution:

				double[] sol = opt.getOptimizationResponse().solution;
				sol[0] = 4/3
				sol[1] = 1/3

Download test source bundle

Download the entire test source bundle from here.