Solver4J – LP - linear programming

A minimization problem in the form of:

  minimize _x c ^Tx+d  s.t.
    Gx ≤ h
    Ax = b,

where G ∈ R ^mXn and A ∈ R ^pXn

is called a linear program (LP). Linear programs are obviously convex optimization problems. You can solve LP with Solver4J viewing them as general convex problems or as a special kind of optimizations, as shown below.

LP as a general convex problem

2D example

Consider the problem graphically represented hereafter: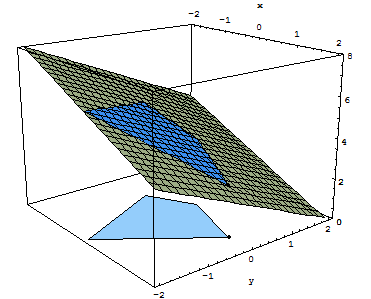

It can be solved like this:

		
		// Objective function (plane)
		LinearMultivariateRealFunction objectiveFunction = new LinearMultivariateRealFunction(new double[] { -1., -1. }, 4);

		//inequalities (polyhedral feasible set G.X<H )
		ConvexMultivariateRealFunction[] inequalities = new ConvexMultivariateRealFunction[4];
		double[][] G = new double[][] {{4./3., -1}, {-1./2., 1.}, {-2., -1.}, {1./3., 1.}};
		double[] h = new double[] {2., 1./2., 2., 1./2.};
		inequalities[0] = new LinearMultivariateRealFunction(G[0], -h[0]);
		inequalities[1] = new LinearMultivariateRealFunction(G[1], -h[1]);
		inequalities[2] = new LinearMultivariateRealFunction(G[2], -h[2]);
		inequalities[3] = new LinearMultivariateRealFunction(G[3], -h[3]);
		
		//optimization problem
		OptimizationRequest or = new OptimizationRequest();
		or.setF0(objectiveFunction);
		or.setFi(inequalities);
		//or.setInitialPoint(new double[] {0.0, 0.0});//initial feasible point, not mandatory
		or.setToleranceFeas(1.E-9);
		or.setTolerance(1.E-9);
		
		//optimization
		Solver4J opt = new Solver4J();
		opt.setOptimizationRequest(or);
		opt.optimize();

This will give the solution:

 double[]
						sol = opt.getOptimizationResponse().getSolution(); sol[0] = 1.5
						sol[1] = 0.0

LP as a special kind of optimization

Given its uncountables fields of application, LP is worth a special threatment that takes into account all the particulars topics and stuctures that are inherents with it. We summarize this in the following:

standard form
LP's can be stated in a standard form wich all of the problems can be reconducted to regardless their original elements. A problem in a standard form is expressed as:
  minimize _x c ^Tx  s.t.
    Ax = b,
    x ≤ 0

where A ∈ R ^pXn
See S.Boyd and L.Vandenberghe, "Convex Optimization", 4.3 for more details. In Solver4J the expression above is referred to as strictly standard form, while the term standard form is used for the more general problem
  minimize _x c ^Tx+d  s.t.
    Ax = b,
    lb ≤ x ≤ ub
The standard form provides the common basis for theoretical argumentations and for practical solvers implementations.
linear presolving
it is possible to leverage the special structure of LP's in order to simplify the problem itself. This involves a lot of techiques based both on deterministics and both on heuristics approaches, so that the problem effectively passed in to the solver can be structurally and numerically more affordable.
KKT solvers
for a given LP, objective function and inequalities hessians are zero, and the H matrix in the KKT system is either diagonal (in the minization phase) or block diagonal (in the Phase I phase), so that special efficient KKT solver can be used to invert the KKT system (see S.Boyd and L.Vandenberghe, "Convex Optimization", 10.4 for more details).
sparse structure
if the problem is stated in terms of sparse data structures, we can leverage it in the linear algebra underlying the optimizers, increasing speed and precision
widespread accepted data format
common file format for storing the data of an LP are emerged as de facto standards among most of the commercial solvers, like for example MPS, AMPL, GAMS. Solver4J can be requested with problems in MPS format.

Solver4J provides the specialized LPOptimizationRequest and LPPrimalDualMethod request and solver to deal with linear problems: the users who are familiar with the Mathematica software can think at the difference bethween these classes and their basic counterparts as the same difference bethween the Solve[] and LinearProgramming[] functions of Mathematica .

Given all this major strengths, this is the recommended way to solve LP problems with Solver4J.

2D example

Here we solve the same problem as above using the specialized classes LPPrimalDualMethod and LPOptimizationRequest

		
		//Objective function
		double[] c = new double[] { -1., -1. };
		
		//Inequalities constraints
		double[][] G = new double[][] {{4./3., -1}, {-1./2., 1.}, {-2., -1.}, {1./3., 1.}};
		double[] h = new double[] {2., 1./2., 2., 1./2.};
		
		//Bounds on variables
		double[] lb = new double[] {0 , 0};
		double[] ub = new double[] {10, 10};
		
		//optimization problem
		LPOptimizationRequest or = new LPOptimizationRequest();
		or.setC(c);
		or.setG(G);
		or.setH(h);
		or.setLb(lb);
		or.setUb(ub);
		or.setDumpProblem(true); 
		
		//optimization
		LPPrimalDualMethod opt = new LPPrimalDualMethod();
		
		opt.setLPOptimizationRequest(or);
		opt.optimize();

This will give the solution:

						double[] sol = opt.getOptimizationResponse().getSolution(); sol[0] = 1.5
						sol[1]
						= 0.0

The Netlib test suite

A very strong effort has been done in order to test Solver4J against the standard Netlib set of LP problems, that since its introduction in 1985 has served as a repository of linear programming instances spanning from simple ones with few variables and constraints to very hard ones with hundreds or thousands variables and constraints. Netlib problems are stated in the widespread MPS format, and Solver4J provides a MPS model parser ( MPSParser ) out-of-the-box. Here we list the problems with dimension < 1000 (number of variables) and give a comparison with the results of Mathematica .

Name	NZ ¹	Rows ²	Cols ³	Expected sol ⁴	Sol	Time(ms) ⁵	Result
adlittle	383	56	97	225494.96316238074	225494.96316388305	1123
afiro	83	27	32	- 464.75314285714285	-464.7531428567392	86
afiroPresolved	36	11	14	- 464.7531388077601	-464.75313880730135	77
agg2	4284	516	302	- 2.023925235453042e7	-2.0239252355975658E7	8276
agg3	4300	516	302	1.0312115935144696e7	1.0312115935089389E7	9840
agg	2410	488	163	- 3.599176723191548e7	-3.5991767286575414E7	3628
bandm	2494	305	472	- 158.62801844112423	-158.62801794084012	4363
beaconfd	3375	173	262	33592.48585404656	33592.48580895807	180
blend	491	74	83	- 30.8121498458288	-30.812149512678396	559
bore3d	1429	233	315	1373.080397008219	1373.0803964471754	865
brandy	2148	220	249	1518.5098962632164	1518.5098965686252	2113
brandyPresolved	1641	104	173	1518.509877 369288	1518.5098749977176	1579
capri	1767	271	353	2690.0129142514993	2690.0129946755874	6977	^*
degen2	3978	444	534	- 1435.1779999618445			^**
e226	2578	223	282	- 18.751929062178103	-18.75192813580968	4028
etamacro	2409	400	688	- 755.7152309967234	-755.7152333591588	9382
fffff800	6227	524	854	555679.5653854093	555679.5648193859	27928
finnis	2310	497	614	172791.06577963303	172791.0655946926	18181
grow15	5620	300	645	- 1.068709412913749e8	-1.068709412935738E8	8067
grow22	8252	440	946	- 1.6083433648256025e8	-1.6083433648256144E8	21511
grow7	2612	140	301	- 4.7787811689099975e7	-4.778781181471146E7	1665
israel	2269	174	142	- 896644.8218546732	-896644.8218626275	3166
kb2	286	43	41	- 1749.9001299062052	-1749.9001292624007	139
lotfi	1078	153	308	- 25.264706060189596	-25.264705441676703	1695
pilot4	5141	410	1000	- 2581.1392582314916	-2581.1392584424075	30150
recipe	663	91	180	-266.616	- 266.6159999770676	335
recipePresolved	359	48	71	- 256.606	-256.60599991024844	112
sc105	280	105	103	- 52.20206121160103	-52.202060736338595	518
sc205	551	205	203	- 52.202061191386655	-52.20206053809183	2303
sc50a	130	50	48	- 64.57507705856449	-64.5750767415132	71
sc50b	118	50	48	-70.	-69.99999866747802	61
scagr25	1554	471	500	-1.4753433060425166e7	-1.4753433060766958E7	3132
scagr7	420	129	140	-2.331389824330984e6	-2331389.8243302316	257
scfxm1	2589	330	457	18416.759028361623	18416.75902885911	7312
scfxm2	5183	660	914	36660.26169940316	36660.261566587586	36606
scorpion	1426	388	358	1878.1248227566775	1878.1248252525409	947
scsd1	2388	77	760	8.666666674333362	8.666667689524276	1468
sctap1	1692	300	480	1412.2500032466096	1412.2500015165754	5304
share1b	1151	117	225	-76589.31857580518	-76589.31857827255	1617
share2b	694	96	79	-415.7322407414194	-415.7322402976527	426
stair	3856	356	467	-251.26695113319397	-251.26695031324036	12494
stocfor1	447	117	111	-41131.97618969361	-41131.97621655949	362
tuff	4520	333	587	0.2921477655844379	0.29215072738855474	4373
vtp-base	908	198	203	129831.46246147664	129831.46246334001	207

NOTE:

¹ total number of non zero elements in the equalities and inequalities constraints matrices
² total number of equalities and inequalities constraints
³ number of variables
⁴ the solution given by Mathematica
⁵ tests are executed on the Java(TM) SE Runtime Environment (build 1.6.0_24-b07) Java HotSpot(TM) 64-Bit Server VM (build 19.1-b02, mixed mode) running on a Win7 Professional OS on an Intel i7 processor pc with 8GB ram.
^* solved with poor convergence norm precision
^** this problem cannot be solved with Solver4J because the equalities constraints matrix is not full rank

The complete Netlib JUnit test set and feed data are available for download here . They are not included in the base source bundle because of the big size of the files. Together with the java code, you can also find all the Mathematica notebooks used for reference.