Solver4J – LFP - linear fractional programming

A minimization problem in the form of:

${minimize}_{x} \frac{c^{T} x + d}{e^{T} x + f}$ s.t.
$Gx < h$
$Ax = b$

with $x \in {x | e^{T} x + f > 0}$

is called a linear-fractional program (LFP). See S.Boyd and L.Vandenberghe, "Convex Optimization", 4.3.2 for more details.

Linear fractional programs are not convex optimization problems because the objective function is quasiconvex (quasilinear precisely) so linear-fractional programs are quasiconvex optimization problems; however, they can be transformed to convex problems by a change of variables and a transformation of the objective and constraint functions. If the feasible set

${x | Gx < h, Ax = b, e^{T} x + f > 0}$

is notempty, LFP can be transformed to the equivalent LP

${minimize}_{x} c^{T} y + dz$ s.t.
     $Gy - hz < 0$
     $Ay - bz = 0$
     $e^{T} y + fz = 1$
     $z = 0$

with variables y, z. Once you have the solution of the LP, the solution in the original variables x is given by x = y/z.

2D example

Consider the problem graphically represented hereafter: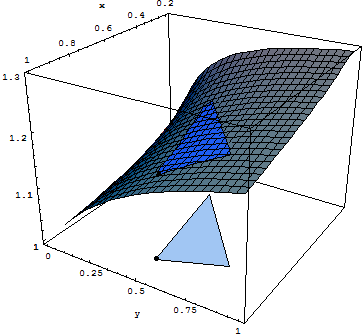

that corresponds to:

${minimize}_{(x, y)} \frac{2x + 4y}{2x + 3y}$ s.t.
$Gx < h$

where

$G = [\begin{matrix} - 1 & 1 \\ 3 & 1 \\ 1 / 5 & - 1 \end{matrix}]$ and $h = [\begin{matrix} 0 \\ 3.2 \\ - 0.32 \end{matrix}]$

It can be solved like this:

		
		// Objective function (variables y0, y1, z)
		double[] n = new double[] { 2., 4., 0.};
		LinearMultivariateRealFunction objectiveFunction = new LinearMultivariateRealFunction(n, 0);

		//inequalities (G.y-h.z<0, z>0)
		double[][] Gmh = new double[][]{{-1.0, 1., 0.},
										{ 3.0, 1.,-3.2},
										{ 0.2,-1., 0.32},
										{ 0.0, 0.,-1.0}};
		ConvexMultivariateRealFunction[] inequalities = new ConvexMultivariateRealFunction[4];
		for(int i=0; i<4;i++){
			inequalities[i] = new LinearMultivariateRealFunction(Gmh[i], 0);
		}
		
		//equalities (e.y+f.z=1)
		double[][] Amb = new double[][]{{ 2.,  3.,  0.}};
		double[] bm= new double[]{1};
		
		//optimization problem
		OptimizationRequest or = new OptimizationRequest();
		or.setF0(objectiveFunction);
		or.setA(Amb);
		or.setB(bm);
		or.setFi(inequalities);
		or.setTolerance(1.E-6);
		or.setToleranceFeas(1.E-6);
		
		//optimization
		Solver4J opt = new Solver4J();
		opt.setOptimizationRequest(or);
		opt.optimize();

This will give the solution:

				double[] sol = opt.getOptimizationResponse().solution;
				sol[0] = 0.2727;
		    sol[1] = 0.1515;
		    sol[2] = 0.3030;

and for the original variables it means:

				x = 0,9
		    y = 0.5

Download test source bundle

Download the entire test source bundle from here.