Solver4J – CCFP - convex-concave fractional programming

A minimization problem in the form of:

${minimize}_{x} \frac{f_{0} (x)}{c^{T} x + d}$ s.t.
$f_{i} (x) < 0, i = 1,. .., m$
$Ax = b$

where $f_{0}, f_{1}, ..., f_{m}$ are convex and the domain of the objective function is defined as ${x \in dom f_{0} | c^{T} x + d > 0}$ , is called a convex-concave-fractional program (CCFP). See S.Boyd and L.Vandenberghe, "Convex Optimization", p. 191 for more details.

Convex-concave fractional program is a quasiconvex optimization problem, but it can be shown that it is equivalent to the convex problem in the new variables $(y, t) \in R^{n} x R$ :

${minimize}_{(y, t)} g_{0} (y, t)$ s.t.
     $g_{i} (y, t) \leq 0, i = 1,. .., m$
     $Ay = bt$
     $c^{T} y + dt = 1$

where

g_{i}

is the perspective of

f_{i}

(if

f : R^{n} \to R

, then the perspective of f is the function

g : R^{n + 1} \to R

defined by

g (x, t) = t f (x / t)

with domain

dom g = \{(x, t) | x / t ∈ dom f, t > 0\}

. See S.Boyd and L.Vandenberghe, "Convex Optimization", p. 89 for more details).

2D example

Consider the problem graphically represented hereafter: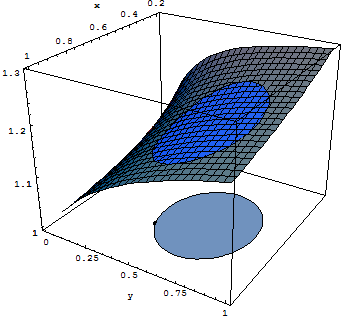

that corresponds to:

${minimize}_{(x, y)} \frac{2x + 4y}{2x + 3y}$ s.t.
${(x - 0.65)}^{2} + {(y - 0.65)}^{2} < {0.25}^{2}$

Note that the objective function is the same as in LFP - 2D example, whereas the inequality constraint has changed from a linear to a quadratic one.
It can be solved like this:

		
		// Objective function (variables y0, y1, t)
		double[] n = new double[] { 2., 4., 0.};
		LinearMultivariateRealFunction objectiveFunction = new LinearMultivariateRealFunction(n, 0);

		//inequalities
		ConvexMultivariateRealFunction[] inequalities = new ConvexMultivariateRealFunction[2];
		//t > 0
		double[][] Gmh = new double[][]{{0.0, 0.0,-1.0}};//t>0
		inequalities[0] = new LinearMultivariateRealFunction(Gmh[0], 0);
		
		//perspective function of (x-c0)^2 + (y-c1)^2 - R^2 < 0
		//this is t*((y0/t - c0)^2 + (y1/t - c1)^2 -R^2)
		//we do not multiply by t, because it would make the function no more convex
		final double c0 = 0.65;
		final double c1 = 0.65;
		final double R = 0.25;
		inequalities[1] = new ConvexMultivariateRealFunction() {
			
			public double value(DoubleMatrix1D X) {
				double y0 = X.getQuick(0);
				double y1 = X.getQuick(1);
				double t =  X.getQuick(2);
				return t * (Math.pow(y0 / t - c0, 2) + Math.pow(y1 / t - c1, 2) - Math.pow(R, 2));
			}
			
			public DoubleMatrix1D gradient(DoubleMatrix1D X) {
				double y0 = X.getQuick(0);
				double y1 = X.getQuick(1);
				double t =  X.getQuick(2);
				double[] ret = new double[3];
				ret[0] = 2 * (y0/t - c0);
				ret[1] = 2 * (y1/t - c1);
				ret[2] = Math.pow(c0, 2) + Math.pow(c1, 2) - Math.pow(R, 2) - (Math.pow(y0, 2) + Math.pow(y1, 2))/Math.pow(t, 2);
				return F1.make(ret);
			}
			
			public DoubleMatrix2D hessian(DoubleMatrix1D X) {
				double y0 = X.getQuick(0);
				double y1 = X.getQuick(1);
				double t =  X.getQuick(2);
				double[][] ret = {
					{                2/t,                   0, -2*y0/Math.pow(t,2)}, 
					{                  0,                 2/t, -2*y1/Math.pow(t,2)}, 
					{-2*y0/Math.pow(t,2), -2*y1/Math.pow(t,2),  2*(Math.pow(y0,2) + Math.pow(y1,2))/Math.pow(t,3)}};
				return F2.make(ret);
			}
			
			public int getDim() {
				return 3;
			}
		};
		
		//equalities (e.y+f.t=1), f is 0
		double[][] Amb = new double[][]{{ 2.,  3.,  0.}};
		double[] bm= new double[]{1};
		
		//optimization problem
		OptimizationRequest or = new OptimizationRequest();
		or.setF0(objectiveFunction);
		or.setA(Amb);
		or.setB(bm);
		or.setFi(inequalities);
		or.setTolerance(1.E-6);
		or.setToleranceFeas(1.E-6);
		or.setNotFeasibleInitialPoint(new double[] { 0.6, -0.2/3., 0.1 });
		or.setCheckKKTSolutionAccuracy(true);
		
		//optimization
		Solver4J opt = new Solver4J();
		opt.setOptimizationRequest(or);
		opt.optimize();

This will give the solution:

				double[] sol = opt.getOptimizationResponse().solution;
				sol[0] = 0.2719;
		    sol[1] = 0.1521;
		    sol[2] = 0.3522;

and for the original variables it means:

				x = 0.772
		    y = 0.431

Download test source bundle

Download the entire test source bundle from here.