Solver4J – QCQP - quadratically constrained quadratic programming

A minimization problem in the form:

  minimize_x (1/2)x^TP₀x+q₀^T+r₀  s.t.
    (1/2)x^TP_ix+q_i^T+r_i ≤ 0,  i=1,...,m
    Ax = b,

where P_i ∈ S₊ⁿ, i=0,...,m, and A ∈ R^pXn

is called a quadratically constrained quadratic program (QCQP). Quadratically constrained quadratic program include quadratic program as a special case by taking P_i=0 for i=1,...,m.

2D example

Consider the problem graphically represented hereafter: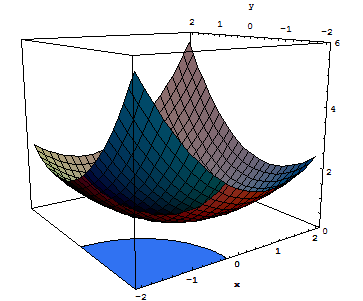

It can be solved like this:

		
		// Objective function
		double[][] P = new double[][] { { 1., 0.4 },{ 0.4, 1. }};
		PDQuadraticMultivariateRealFunction objectiveFunction = new PDQuadraticMultivariateRealFunction(P, null, 0);

		//inequalities
		ConvexMultivariateRealFunction[] inequalities = new ConvexMultivariateRealFunction[1];
		inequalities[0] = FunctionsUtils.createCircle(2, 1.75, new double[]{-2, -2});
		
		//optimization problem
		OptimizationRequest or = new OptimizationRequest();
		or.setF0(objectiveFunction);
		or.setInitialPoint(new double[] { -2., -2.});
		or.setFi(inequalities);
		or.setCheckKKTSolutionAccuracy(true);
		
		//optimization
		Solver4J opt = new Solver4J();
		opt.setOptimizationRequest(or);
		opt.optimize();

This will give the solution:

				double[] sol = opt.getOptimizationResponse().solution;
				sol[0] = -2 + 1.75/Math.sqrt(2)
				sol[1] = -2 + 1.75/Math.sqrt(2)

Download test source bundle

Download the entire test source bundle from here.